Critical Value StatCrunch: Master it in Minutes! [Guide]

Understanding statistical analysis often requires proficiency in using tools like StatCrunch. A crucial step in many statistical tests involves determining the critical value, and this is where effective tool usage becomes essential. Whether you're working with hypothesis testing or confidence intervals, knowing how to find the critical value on StatCrunch is paramount for accurate conclusions. Pearson Education, a leading provider of educational resources, provides materials covering the importance of critical values in statistical applications, underlining their relevance in both academic and professional settings.

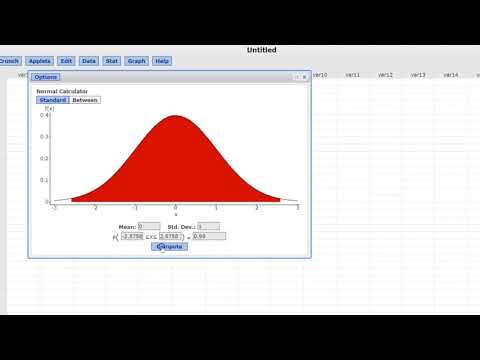
Image taken from the YouTube channel KOLA STATS , from the video titled Finding Critical Values using Statcrunch. .

Decoding Critical Values in StatCrunch: Your Quick Guide

This guide provides a clear and concise walkthrough on using StatCrunch to find critical values, especially focusing on scenarios where you need to understand and apply the concept. Our core focus is on detailing how to find the critical value on StatCrunch.

Understanding Critical Values: The Foundation

Before diving into StatCrunch, let's establish what a critical value is and why it's important. A critical value is a point on the scale of the test statistic beyond which we reject the null hypothesis. It determines the boundary between values that would lead us to reject the null hypothesis and those that wouldn't.

• Significance Level (α): The probability of rejecting the null hypothesis when it is actually true (Type I error). Commonly 0.05, 0.01, or 0.10.
• One-tailed vs. Two-tailed Tests: The directionality of the hypothesis test impacts how critical values are determined. One-tailed tests consider only one direction (either greater than or less than), while two-tailed tests consider both.

Locating Critical Values on StatCrunch: Step-by-Step

Now, let's get practical. Here's how to find critical values using StatCrunch, broken down by common statistical tests:

Z-Critical Values (For Z-tests)

The Z-critical value is used when your test statistic follows a standard normal distribution.

1. Open StatCrunch: Launch the StatCrunch software.
2. Navigate to Calculator: Go to Stat > Calculators > Normal.
3. Select "Standard": Make sure the distribution is set to Standard (mean = 0, standard deviation = 1).
4. One-tailed Test:
   • If the test is right-tailed (greater than): Select > and enter 1 - α in the probability box (e.g., for α = 0.05, enter 0.95). The corresponding Z-value will be displayed.
   • If the test is left-tailed (less than): Select < and enter α in the probability box (e.g., for α = 0.05, enter 0.05). The corresponding Z-value will be displayed.
5. Two-tailed Test:
   • Divide the significance level by 2: α/2 (e.g., for α = 0.05, α/2 = 0.025).
   • Find the Z-value for the lower tail: Select < and enter α/2 in the probability box (e.g., enter 0.025). Note the Z-value (it will be negative).
   • The Z-value for the upper tail is the positive version of the Z-value you just found.

T-Critical Values (For T-tests)

The T-critical value is used when your test statistic follows a T-distribution. You'll need to know the degrees of freedom (df).

1. Open StatCrunch: Launch the StatCrunch software.
2. Navigate to Calculator: Go to Stat > Calculators > T.
3. Enter Degrees of Freedom: Enter the correct degrees of freedom for your T-test in the df box. (Degrees of freedom is usually calculated as sample size - 1).
4. One-tailed Test:
   • If the test is right-tailed (greater than): Select > and enter 1 - α in the probability box (e.g., for α = 0.05, enter 0.95). The corresponding T-value will be displayed.
   • If the test is left-tailed (less than): Select < and enter α in the probability box (e.g., for α = 0.05, enter 0.05). The corresponding T-value will be displayed.
5. Two-tailed Test:
   • Divide the significance level by 2: α/2 (e.g., for α = 0.05, α/2 = 0.025).
   • Find the T-value for the lower tail: Select < and enter α/2 in the probability box (e.g., enter 0.025). Note the T-value (it will be negative).
   • The T-value for the upper tail is the positive version of the T-value you just found.

Chi-Square Critical Values (For Chi-Square Tests)

The Chi-Square critical value is used for Chi-Square tests, which are often employed for analyzing categorical data. Again, you'll need to know the degrees of freedom (df).

1. Open StatCrunch: Launch the StatCrunch software.
2. Navigate to Calculator: Go to Stat > Calculators > Chi-square.
3. Enter Degrees of Freedom: Enter the correct degrees of freedom for your Chi-Square test in the df box. Degrees of freedom depends on the specific chi-square test being performed.
4. Finding the Critical Value: Chi-Square tests are usually right-tailed. Select > and enter 1 - α in the probability box (e.g., for α = 0.05, enter 0.95). The corresponding Chi-Square value will be displayed.

F-Critical Values (For ANOVA)

The F-critical value is used for F-tests, primarily in Analysis of Variance (ANOVA). You'll need two sets of degrees of freedom: numerator degrees of freedom (df numerator) and denominator degrees of freedom (df denominator).

1. Open StatCrunch: Launch the StatCrunch software.
2. Navigate to Calculator: Go to Stat > Calculators > F.
3. Enter Degrees of Freedom: Enter the degrees of freedom for the numerator in the df numerator box and the degrees of freedom for the denominator in the df denominator box.
4. Finding the Critical Value: F-tests are typically right-tailed. Select > and enter 1 - α in the probability box (e.g., for α = 0.05, enter 0.95). The corresponding F-value will be displayed.

Practical Examples

Let's illustrate with some specific examples to solidify your understanding.

• Example 1: Finding the Z-critical value for a right-tailed test with α = 0.01. In StatCrunch, use the Normal calculator, select >, and enter 0.99. The displayed Z-value (approximately 2.33) is your critical value.
• Example 2: Finding the T-critical value for a two-tailed test with α = 0.05 and df = 20. In StatCrunch, use the T calculator, enter 20 for df, select <, and enter 0.025. The T-value will be negative (approximately -2.086). The positive value, 2.086, is your upper-tail critical value.

By understanding these steps and examples, you'll be well-equipped to efficiently and accurately find critical values using StatCrunch for a variety of statistical tests.

Video: Critical Value StatCrunch: Master it in Minutes! [Guide]

Play Video