BCC Unit Cell Volume: The Simple Guide You Must Know!

Understanding the body-centered cubic (BCC) unit cell is fundamental in materials science. This structure, often studied at institutions like the Massachusetts Institute of Technology (MIT), dictates many material properties. The atomic packing factor is intrinsically linked to the overall structure, and its determination often relies on accurately calculating the volume of BCC unit cell in terms of r, where 'r' represents the atomic radius. Finally, the effective employment of X-ray diffraction techniques allows for the experimental verification and precise determination of the lattice parameters, thus confirming theoretical calculations of the volume of BCC unit cell in terms of r.

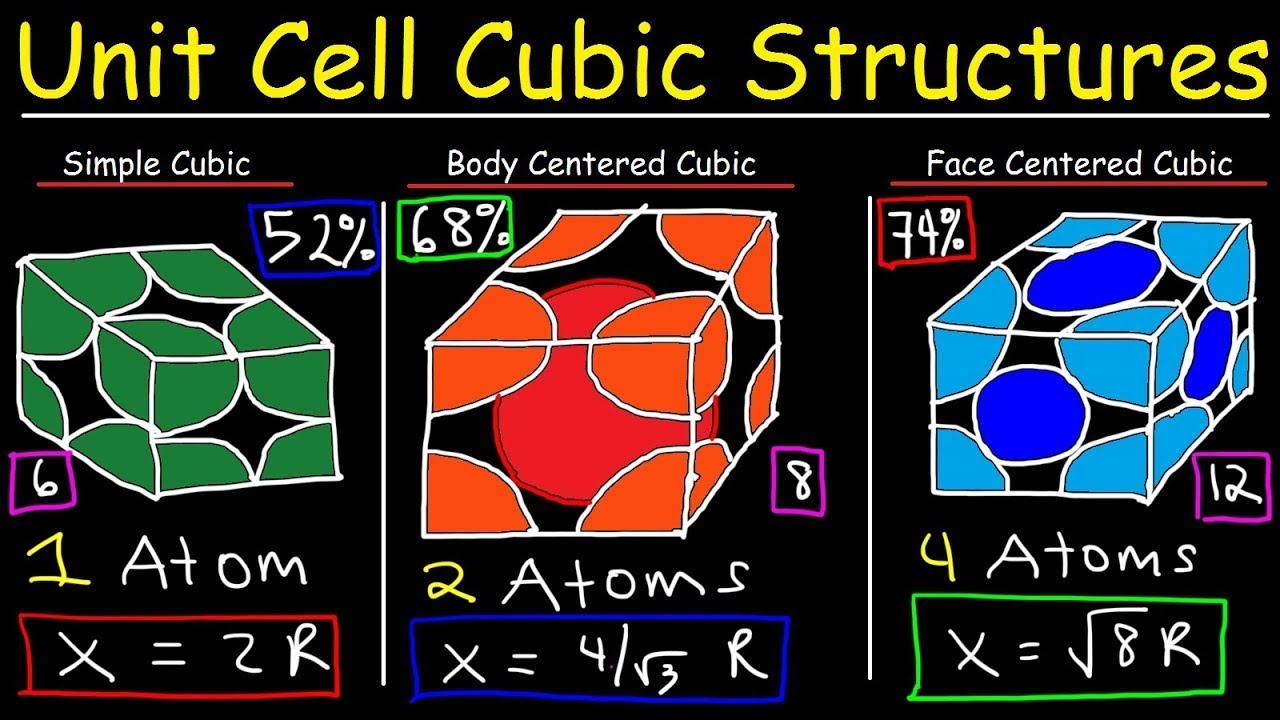
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Unit Cell Chemistry Simple Cubic, Body Centered Cubic, Face Centered Cubic Crystal Lattice Structu .

Materials science stands as a cornerstone of modern technology, driving innovation in fields ranging from aerospace engineering to biomedical devices. At the heart of this discipline lies the understanding of crystal structures, the ordered arrangements of atoms that dictate a material's properties. Among these structures, the Body-Centered Cubic (BCC) lattice holds a prominent position.

Exploring Body-Centered Cubic (BCC) Crystal Structures

BCC structures are characterized by an arrangement of atoms with one atom at each of the eight corners of a cube and an additional atom located at the cube's center. This seemingly simple arrangement has profound implications for the material's mechanical, thermal, and electrical behavior. Many technologically important metals, such as iron, chromium, and tungsten, crystallize in the BCC structure. Their strength, ductility, and high-temperature performance are intimately linked to this atomic arrangement.

Purpose: Unlocking the Volume Calculation

This exploration aims to provide a clear and concise explanation of how to calculate the volume of a BCC unit cell, expressing it directly in terms of the atomic radius (r). The unit cell is the smallest repeating unit of the crystal lattice, and knowing its volume is crucial for understanding macroscopic material properties.

Why This Matters: Characterization and Prediction

The relationship between the BCC unit cell volume and the atomic radius is more than just a geometrical curiosity. It is a powerful tool that enables:

• Materials Characterization: By knowing the atomic radius of a material, we can estimate the size of its unit cell, which then helps determine density and other crucial properties.

• Properties Prediction: The volume of the unit cell directly influences the packing efficiency of atoms within the crystal structure. This in turn affects the material's strength, its ability to deform, and its resistance to corrosion. The knowledge allows us to predict the behavior of materials under various conditions.

In essence, mastering this calculation unlocks a deeper understanding of the connection between atomic-scale structure and macroscopic material behavior.

Materials characterization and property prediction rely heavily on a solid understanding of a material's atomic arrangement. To grasp the significance of the volume calculation, we must first delve into the fundamental building block upon which these crystal structures are built. This brings us to the concept of the unit cell and its specific manifestation in the BCC lattice.

Understanding the BCC Unit Cell: The Building Block

At the heart of every crystalline material lies a repeating structural motif known as the unit cell.

Think of it as a LEGO brick – a single, identical component that, when replicated and arranged in three-dimensional space, creates the entire structure.

The unit cell is the smallest representation of the crystal lattice, encapsulating its symmetry and atomic arrangement.

Defining the Unit Cell

The unit cell is defined as the smallest repeating unit of a crystal lattice that, when translated in three dimensions, generates the entire crystal structure.

It is characterized by its dimensions (edge lengths a, b, and c) and the angles between these edges (α, β, and γ). These parameters fully describe the unit cell's geometry.

Imagine tiling a floor: the unit cell is the individual tile shape that, when repeated, covers the entire floor without gaps or overlaps.

The BCC Arrangement: Atoms in a Cube

The Body-Centered Cubic (BCC) unit cell is a specific type of cubic unit cell with a distinctive atomic arrangement.

As the name suggests, it features an atom at each of the eight corners of a cube, and one additional atom located at the very center of the cube.

It's crucial to visualize this: the corner atoms are shared with adjacent unit cells, meaning only a fraction of each corner atom belongs to the specific unit cell under consideration.

Visualizing the BCC Structure

To fully understand the BCC structure, consider these key geometrical features:

• Corner Atoms: Eight atoms located at the corners of the cube. Each corner atom is shared by eight adjacent unit cells, so only 1/8 of each corner atom belongs to a given unit cell. This contributes a total of 1 atom (8 corners * 1/8 atom/corner = 1 atom) to the unit cell.

• Center Atom: One atom located at the center of the cube. This atom belongs entirely to the unit cell.

  You also like

  Decoding: Nicholas Braun Perks Wallflower Char! Viral!

Therefore, a BCC unit cell contains a total of two atoms (one from the corners and one at the center).

A helpful visualization is to imagine a transparent cube with spheres representing atoms placed at each corner and in the center.

This mental image clarifies the spatial arrangement of atoms within the BCC lattice and facilitates a better understanding of its properties.

Materials characterization and property prediction rely heavily on a solid understanding of a material's atomic arrangement. To grasp the significance of the volume calculation, we must first delve into the fundamental building block upon which these crystal structures are built. This brings us to the concept of the unit cell and its specific manifestation in the BCC lattice.

Atomic Radius (r) and Lattice Constant (a): Establishing the Connection

The size of the BCC unit cell is dictated by the lattice constant, often denoted as 'a'. This constant represents the length of one side of the cubic unit cell.

However, the lattice constant alone doesn't fully describe the atomic packing within the structure. We need to relate it to the atomic radius (r) of the constituent atoms. This connection unlocks our ability to calculate the unit cell volume directly from the atomic properties.

The relationship between the atomic radius (r) and the lattice constant (a) in a BCC structure is a cornerstone of understanding its geometry and, consequently, its properties. The formula that governs this relationship is:

a = 4r / √3

This seemingly simple equation holds the key to unlocking a deeper understanding of BCC materials. Let's embark on a step-by-step journey to derive this formula, supported by clear geometric reasoning and illustrative diagrams.

Step-by-Step Derivation of the Relationship

The derivation of a = 4r / √3 relies on understanding how atoms touch within the BCC unit cell. It’s crucial to visualize the atoms making contact along the body diagonal of the cube.

Visualizing the Atomic Contact

Imagine a line drawn from one corner of the cube, through the center atom, to the opposite corner. Along this line, there are three atoms:

• An atom at the starting corner.
• The atom located at the center of the cube.
• An atom at the opposite corner.

These atoms touch each other along this diagonal, meaning their radii are directly related to the length of the diagonal. This is the key to unlocking the formula.

Applying the Pythagorean Theorem (Twice!)

To find the length of the body diagonal, we can utilize the Pythagorean theorem in a two-step process.

Step 1: Finding the Face Diagonal

First, consider a face of the cube. The diagonal of this face can be calculated as follows:

• Let the face diagonal be 'f'.
• According to the Pythagorean theorem: f² = a² + a² = 2a²
• Therefore, f = √(2a²) = a√2

Step 2: Finding the Body Diagonal

Now, consider the right triangle formed by one edge of the cube (length 'a'), the face diagonal ('f' = a√2), and the body diagonal (which we'll call 'd'). Again, applying the Pythagorean theorem:

• d² = a² + f² = a² + (a√2)² = a² + 2a² = 3a²
• Therefore, d = √(3a²) = a√3

Relating the Body Diagonal to the Atomic Radius

We know that the body diagonal (d) is equal to a√3. We also know that it's equal to four times the atomic radius (4r), since there are two corner radii and one full diameter of the center atom along the diagonal.

Equating these two expressions, we get:

• a√3 = 4r

Solving for 'a', we arrive at the final relationship:

• a = 4r / √3

This equation demonstrates the direct link between the atomic radius 'r', a fundamental property of the atom, and the lattice constant 'a', which defines the size of the BCC unit cell.

Calculating the BCC Unit Cell Volume: The Formula Unveiled

Having established the vital link between the atomic radius (r) and the lattice constant (a) in a BCC structure, we are now perfectly positioned to determine the BCC unit cell volume.

This calculation brings together fundamental geometric principles with the specific atomic arrangement characteristic of BCC lattices.

From Cube to Formula: Recalling Basic Geometry

The unit cell, as we've discussed, is a cube.

Therefore, its volume is calculated using the familiar formula:

Volume = a³

This is a fundamental geometric principle and serves as our starting point.

Substituting the Relationship: Bridging 'a' and 'r'

The crucial step now is to incorporate the relationship we previously derived: a = 4r / √3.

This equation allows us to express the volume of the unit cell solely in terms of the atomic radius (r).

Substituting this into the volume formula, we get:

Volume = (4r / √3)³

This substitution directly connects the macroscopic volume to the microscopic atomic property, the radius.

Simplifying the Expression: Unveiling the Final Formula

The next step involves careful algebraic simplification.

Expanding the expression, we have:

Volume = (4r)³ / (√3)³ Volume = 64r³ / (3√3)

Therefore, after simplification, we arrive at the final formula for the volume of a BCC unit cell in terms of r:

Volume = (64r³) / (3√3)

The Final Formula: A Concise Representation

This is the key result.

This equation provides a direct means of calculating the volume of a BCC unit cell, knowing only the atomic radius of the constituent atoms.

This formula provides a critical bridge between atomic-scale properties and the macroscopic behavior of BCC materials.

Real-World Significance and Applications of BCC Volume

The formula for BCC unit cell volume, derived from fundamental geometric principles, transcends theoretical curiosity and becomes a powerful tool in materials science. Understanding this volume unlocks insights into a material’s behavior, from its strength and ductility to its thermal and electrical conductivity.

Linking Volume to Material Properties

The volume of the BCC unit cell is intrinsically linked to several key material properties. For instance, a smaller unit cell volume generally implies a higher density, assuming similar atomic masses. Density, in turn, influences a material’s weight, strength, and resistance to corrosion.

Furthermore, the volume affects the number of atoms per unit volume, directly impacting properties like yield strength and hardness. A higher atomic density can lead to increased resistance to plastic deformation, because more atoms are present to resist dislocation movement.

Unveiling Packing Efficiency

Knowing the BCC unit cell volume is crucial for determining its atomic packing factor (APF). APF represents the percentage of space within the unit cell occupied by atoms. For BCC structures, the APF is approximately 0.68, meaning only 68% of the space is filled, and the rest is empty.

This relatively lower packing efficiency (compared to face-centered cubic structures) influences the ease with which atoms can move through the lattice. This affects diffusion rates and, consequently, temperature-dependent properties like creep resistance and sintering behavior.

A lower packing efficiency can also influence the material's ability to absorb energy during impacts.

Examples in the World Around Us

Several technologically important metals exhibit the BCC structure, each leveraging its unique atomic arrangement to achieve specific properties:

• Iron (Fe): Pure iron, and especially ferritic steels (BCC iron with carbon), are widely used structural materials due to their high strength and relatively low cost. The BCC structure contributes to iron's ferromagnetic properties below its Curie temperature.

• Chromium (Cr): Chromium is often added to steel to improve its corrosion resistance. Its BCC structure contributes to the formation of a passive oxide layer, protecting the underlying metal from degradation.

• Tungsten (W): Tungsten's extremely high melting point and strength at elevated temperatures make it ideal for applications like light bulb filaments and high-temperature alloys. Its BCC structure contributes to its exceptional high-temperature performance.

These examples showcase how the seemingly simple concept of BCC unit cell volume plays a critical role in determining the suitability of a material for a given engineering application. By understanding this fundamental property, materials scientists and engineers can design and tailor materials with specific characteristics to meet the demands of modern technology.

Video: BCC Unit Cell Volume: The Simple Guide You Must Know!

Play Video